Tehokas reduce

Funktionaalisen ohjelmoinnin kolme keskeisintä työkalua ovat eittämättä korkeamman asteen funktiot map, reduce ja filter, joista kullakin on omanlaisensa tehtävä. Näistä kuitenkin reduce voittaa yleisyydessä kevyesti.

Esittelen tässä postauksessa funktionaalisten kielten perusteisiin kuuluvana asiana kuinka nämä funktiot voitaisiin kirjoittaa ja sitten, miten reduce voi korvata sekä map-, että filter-funktiot.

map

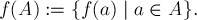
Funktio map on niin klassinen työväline listojen käsittelyssä, että se tuntuu uponneen kertaheitolla kaaliin. Matemaattisesti map ei ole paljoa muuta kuin funktion soveltaminen kokonaiseen joukkoon, usein kirjoitettuna näin: $$f(A) := \{ f(a) \mid a \in A \}.$$

Funktionaaliset kielet pelaavat jonojen, usein listojen parissa. Siispä matemaattinen joukkonotaatio ja joukkojen kanssa puljautuminen siirtyy listoiksi. Clojure osaa toki soveltaa map-funktiota joukkoihinkin, koska joukot toteuttavat yleisemmän jonoabstraktion.

map ottaa siis tavallisesti kaksi argumenttia; ensin käytettävän funktion ja toisena kokoelman alkioita, joihin funktiota sovelletaan. Clojuressa kokoelmia saa toimittaa mielivaltaisen monta. Tällöin kustakin joukosta poimitaan kerralla yksi argumentti annettavaksi funktiolle.

Funktionaaliseen tapaan kirjoitamme toteutukset rekursiiviseen tapaan. 

(defn map [fun coll]
  (loop [fun fun, coll (seq coll), acc ()]
    (if-let [x (first coll)]
      (recur fun
             (rest coll)
             (concat acc (list (fun x))))
      acc)))

(defn map' [fun coll]
  (if-let [x (first coll)]
    (cons (fun x)
          (map' fun (rest coll)))))

Tässä on kaksi naiivia, perustason esimerkkiä, miten map:n voisi toteuttaa. Ensimmäinen käyttää rekursiivisuuteen Clojuren toteuttamaa loop-recur -rakennetta, jolla häntärekursio saadaan kuriin. Tuloksena on myös hieman rumempaa koodia.

Toinen tapa on perinteisempi funktionaalinen tapa, jota Haskell-ihmiset varmasti muistavat kehua. Rakennamme hyvin perinteisellä cons-metodilla saman listan. cons eli construct lisää ensimmäisen argumenttinsa toisen argumentin alkuun.

Haskellissa on vastaavanlainen listojen rakennusmenetelmä, eli lyhyt oppimäärä: $x : [a, b, c] == [x, a, b, c]$. Kaksoispiste : toimii konstruktorina. Tästä sitten rekursiivisesti voimme sanoa, että $1 : 2 : 3 : []$ on sama lista kuin $[1, 2, 3]$. Ylimääräiset sulut voimme näet jättää pois tässä yhteydessä.

Yhtä kaikki, JVM ei tue häntärekursiota, eli jälkimmäinen menetelmä kannattaa suosiolla unohtaa. Liian isojen kokoelmien kanssa kutsupino kasvaa ylitse. Clojure valitsi eksplisiittisen merkinnän, loop--recur, jolla optimoitavissa oleva rekursio voidaan ilmaista. Clojuren oikea map-toteutus käyttää laiskoja listoja ja niiden kanssa käytettävää makrorakennetta, ja se on kokonaan toisennäköinen.

filter

Kokoelman suodatus epäkelvon aineksen pyyhkimiseksi on myös eräs hyvin yleinen probleema. filter jättää siis kaikki ne alkiot kokoelmasta jäljelle, joille predikaatti antaa toden.

Ohessa seuraa edellistä map-koodia mukaileva ratkaisu. Pilkullinen versio on taasen se naivi esitys matemaattisesta ideasta taustalla. Jos alkio täyttää ehdon, otetaan se mukaan ja haetaan sitten loput filtteröidyt alkiot uuden kutsun voimin. Eri kätevää. 

(defn filter [pred coll]
  (loop [pred pred, coll coll, acc ()]
    (if-let [x (first coll)]
      (if (pred x)
        (recur pred (rest coll) (concat acc (list x)))
        (recur pred (rest coll) acc))
      acc)))

(defn filter' [pred coll]
  (if-let [x (first coll)]
    (if (pred x)
      (cons x (filter' pred (rest coll)))
      (filter' pred (rest coll)))))

reduce

Reduktiot kokoelmista yhdeksi skalaariksi. Yleisiä ongelmia. Haskellissa foldl, Rubyssä inject ja muissa kielissä reduce tekee homman.

reduce tarvitsee kahden muuttujan funktion, jolle se syöttää aina uuden alkion kokoelmasta. Kertymämuuttuja alustetaan yleensä funktiolle ominaisen neutraalialkion kanssa: yhteenlaskun tapauksessa 0 on luonnollinen, tulon kanssa 1, ja sitä rataa.

Kun ovelana käytämme alkuarvoa x0 myös kertymämuuttujana, saamme itse asiassa aikaan kaikkein sievintä koodia: 

(defn reduce [fun x0 coll]
  (if-let [x (first coll)]
    (recur fun (fun x0 x) (rest coll))
    x0))

Kaikilla näillä funktioilla on määrittelyssä yhteisiä piirteitä: kaikista otetaan ensialkio talteen, ja jos ei saada sellaista niin rekursio lopetetaan (joukko coll on selvästi tyhjä siinä pisteessä).

reduce voittaa

Pienellä notkeudella tutkikaamme, miten map- ja filter-funktiot voisi toteuttaa reduce:n avulla. Meidän tarvitsee vain kirjoittaa sopivanlainen funktio ja alkuarvo lähetettäväksi.

map reduce:n avulla

map kuvaa funktiolla joukon toisenlaiseksi joukoksi: reduktio-funktiomme voisi olla tämännäköinen: 

(defn mapr [fun coll]
  (let [f (fn [xs x]
            (concat xs (list (fun x))))]
    (reduce f () coll)))

Vaikka reduce toimii idealla "kokoelma yhdeksi skalaariksi", on Clojuressa skalaarin käsite hieman häilyvä. Funktiomme palauttaa itse asiassa koko listan plus yhden uuden (ja käsitellyn) alkion, täten replikoiden map-funktion toiminnallisuuden.

filter reduce:n avulla

Samalla menettelyllä kirjoitetaan filter. 

(defn filterr [pred coll]
  (let [f (fn [xs x]
            (if (pred x)
              (concat xs (list x))
              xs))]
    (reduce f () coll)))

Syntyy tavallaan jopa alkuperäistä sievempää koodia.

Mitä tästä opimme?

Että nyt kaikki kirjoittamaan reduktioita? Ei. Yksi asia, missä map ja filter eroavat kovasti tosielämän reduce:sta on niiden laiskuus. Laiskuutta en tässä voinut demonstroida, mutta reduce on määritelmältään epälaiska funktio. Sen on saatava evaluoitua kaikki annetut argumenttinsa, jotta se pääsee suoriutumaan.

Tärkeämpää on ottaa opikseen näistä esimerkeistä reduce:n voima. Esimerkkinä useiden kuvausten yhdistäminen: ennen tätä oppimäärää olisin luultavasti tyytynyt siihen seikkaan, että clojuren oma merge-funktio toimii vain kahden kuvauksen kanssa, ja olisin kirjoittanut loop-recur-rakenteen yhdistämään mielivaltaisen monta kuvausta keskenään. Nyt voin kutsua yksinkertaisemmin: (reduce merge my-maps), ja siirtyä muihin ongelmiin.

Se, että reduce:a aina opetetaan käyttämällä oikeita skalaareja, saattaa hämätä itse kutakin. Kaikki on mahdollista, vaikkapa funktiokompositiokin, saada aikaan reduce:n voimin.

Kommentit, kehitysehdotukset ja keskustelunavaukset ovat tervetulleita sähköpostitse.